| [ < ] |
Maxima ist ein mächtiges Werkzeug für algebraische Manipulationen. Es beherrscht wichtige Funktionen der Mathematik und Physik und kann auch Funktionen (2D, 3D, Vektorfelder) darstellen.
Eine weitere Möglichkeit besteht im Nutzen der Seite http://maxima-online.org/ . Dort kann on-line ein Maxima im Clientbetrieb genutzt werden.
Ein Tutorial gibt es beispielsweise hier.
Wertzuweisung erfolgt durch ":",Beispiel
a : b ;
weist a den Wert b zu.
NB: Ein Strichpunkt wird verwendet, um die Anweisung abzuschliessen. Die Anweisung kann sich auch über mehrere Zeilen erstrecken.
Deklaration einer Funktion durch ":=", Beispiel
f(a) := a^2 ;
oder
y(b) := b+1 ;
Lineare Interpolation, hierbei wird von zwei Wertepaaren (x0,y0) und (x1,y1) ausgegangen.
(%i1) load("interpol")$
(%i2) /* Erzeuge eine Liste p von Punkten */
p : [[x0,y0],[x1,y1]];
(%o2) [[x0, y0], [x1, y1]]
(%i3) lagrange(p);
(x0 - x) y1 + (x - x1) y0
(%o3) - -------------------------
x1 - x0
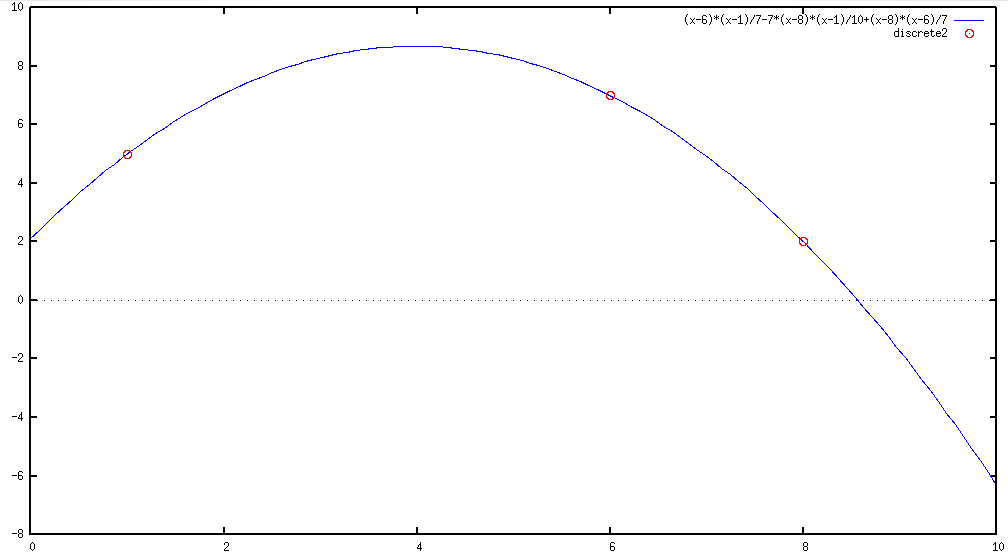
Quadratische Interpolation. Hierzu wird von drei Wertepaaren ausgegangen.
(%i1) load("interpol")$
(%i2) p:[[8,2],[1,5],[6,7]]$
(%i3) lagrange(p);
2
29 x - 231 x - 148
(%o3) - -------------------
70
(%i4) f(x):=''%;
2
29 x - 231 x - 148
(%o4) f(x) := - -------------------
70
(%i5) /* Berechne das Polynom an 3 Stellen */
map(f,[ 2.3 , 5/7 , %pi]);
2
7306 29 %pi - 231 %pi - 148
(%o5) [7.512714285714285, ----, - -----------------------]
1715 70
(%i6) /* Plotte das Polynom zusammen mit den Punkten */
plot2d([f(x),[discrete,p]],[x,0,10],[style, lines, points])$

Trapezregel
(%i1) trapez(f,a,b,n):=(b-a)/(n-1)*(f(b)/2+f(a)/2+sum(f(a+((b-a)/(n-1)*i)),i,1,n-2));
b - a f(b) f(a)
(%o1) trapez(f, a, b, n) := ----- (---- + ----
n - 1 2 2
b - a
+ sum(f(a + ----- i), i, 1, n - 2))
n - 1
(%i2) trapez(sin,0,%pi,10),numer;
(%o2) 1.979650811216483
(%i3) trapez(sin,0,%pi,100),numer;
(%o3) 1.999832163893992
(%i4) trapez(sin,0,%pi,1000),numer;
(%o4) 1.999998351770848
(%i5) integrate(sin(x),x,0,%pi);
(%o5) 2
Simpsonregel
Wichtig: Ungerade Anzahl von Stützstellen (quadratische Interpolation).
(%i1) simpson(f,a,b,n):=(b-a)/(3.0*(n-1))*(f(b)+f(a) \
+2*sum(f(a+((b-a)/(n-1))*2*i),i,1,(n-1)/2-1) \
+4*sum(f(a+((b-a)/(n-1))*(2*i-1)),i,1,(n-1)/2));
b - a
(%o1) simpson(f, a, b, n) := -----------
3.0 (n - 1)
b - a n - 1
(f(b) + f(a) + 2 sum(f(a + ----- 2 i), i, 1, ----- - 1)
n - 1 2
b - a n - 1
+ 4 sum(f(a + ----- (2 i - 1)), i, 1, -----))
n - 1 2
(%i2) simpson(sin,0,%pi,3),numer;
(%o2) 2.094395102393195
(%i3) simpson(sin,0,%pi,9),numer;
(%o3) 2.000269169948388
(%i4) simpson(sin,0,%pi,15),numer;
(%o4) 2.000028343551469
(%i5) simpson(sin,0,%pi,21),numer;
(%o5) 2.000006784441801
(%i6) simpson(sin,0,%pi,101),numer;
(%o6) 2.000000010824504
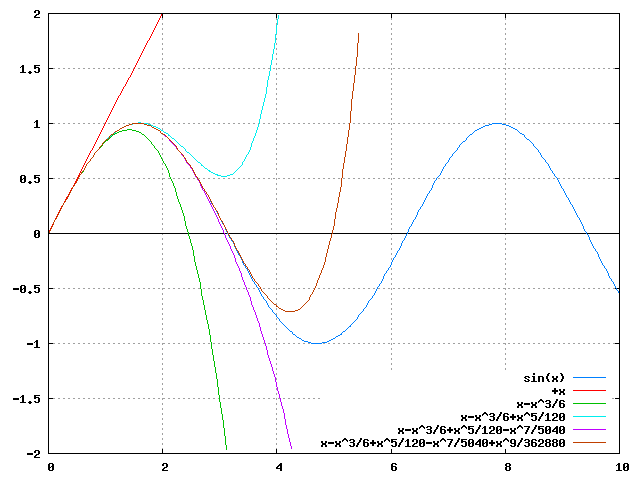
Entwickle sin(x) bis zum neunten Glied. Plotte danach die Funktion sin(x) und Taylorreihenentwicklungen aufsteigender Ordnung.
(%i1) taylor(sin(x), x, 0, 9);
3 5 7 9
x x x x
(%o1)/T/ x - -- + --- - ---- + ------ + . . .
6 120 5040 362880
(%i2) plot2d(append([sin(x)],makelist(taylor(sin(x),x,0,2*i-1),i,1,5)),[x,0,10],[y,-2,2]);
Berechne die Binome (a+b)^n mit den Potenzen n = 0-7. - Pascalsches Dreieck.
(%i1) expand ((a+b)^0);
(%o1) 1
(%i2) expand ((a+b)^1);
(%o2) b + a
(%i3) expand ((a+b)^2);
2 2
(%o3) b + 2 a b + a
(%i4) expand ((a+b)^3);
3 2 2 3
(%o4) b + 3 a b + 3 a b + a
(%i5) expand ((a+b)^4);
4 3 2 2 3 4
(%o5) b + 4 a b + 6 a b + 4 a b + a
(%i6) expand ((a+b)^5);
5 4 2 3 3 2 4 5
(%o6) b + 5 a b + 10 a b + 10 a b + 5 a b + a
(%i7) expand ((a+b)^6);
6 5 2 4 3 3 4 2 5 6
(%o7) b + 6 a b + 15 a b + 20 a b + 15 a b + 6 a b + a
(%i8) expand ((a+b)^7);
7 6 2 5 3 4 4 3 5 2 6 7
(%o8) b + 7 a b + 21 a b + 35 a b + 35 a b + 21 a b + 7 a b + a
Beispiele für die Polynomdivision einer unecht gebrochenen rationalen Funktion. Hierbei benutzt man die generische Funktion "divide".
(%i1) divide( (3*x^3-2*x^2+x-2), (x^2-5*x-2)); (%o1) [3 x + 13, 72 x + 24]Das Resultat is eine Liste. Der erste Bestandteil der Liste steht für den ganzen Anteil, der zweite für den Rest.
(%i2) divide( (x^3-x^2+5) , (x^2-1)); (%o2) [x - 1, x + 4]
(%i3) divide ( (3*x^4-x^2+1) , (x^3+x)); 2 (%o3) [3 x, 1 - 4 x ]
Darstellung einer verschobenen Parabel.
(%i1) plot2d (x^2-6*x+9 ,[x,-5,5] ); (%o1) (%i2) plot2d (3*x^2-2.5*x ,[x,-5,5] ); (%o2) (%i3) plot2d (0.5*x^2-3*x+13 ,[x,-10,10] ); (%o3) (%i4) plot2d (-2*x^2-3*x+13 ,[x,-10,10] );Der Faktor vor dem Quadrat gibt die Öffnung der Parabel an. Ist der Faktor vor dem Quadrat > 0 , so ist die Parabel nach oben geöffnet.Ist der Faktor < 0 , so ist die Parabel nach unten geöffnet.An der Scheitelpunktform f:x => a(x+d)^2 +e ist der Scheitelpunkt S(-d,e) direkt ablesbar. Formt man zb. die Funktion f:x => -2x^2 - 3x + 13 durch quadratische Ergänzung auf die Scheitelpunktform -2(x+0.75)^2 +14.125 um, so ist der Scheitel S(-0.75,14.125) direkt ablesbar.
Rekursion am Beispiel der Fakultät durch selbstdefinierte rekursive Funktion fac(n). Maximas interne Funktion zur Berechnung der Fakultät wird über "n!" angesprochen.
(%i1) fac(n) := if n>0 then fac(n-1)*n elseif n = 0 then 1 ; (%o1) fac(n) := if n>0 then fac(n-1)*n elseif n = 0 then 1 (%i2) fac(5); (%o2) 120 (%i3) fac(7); (%o3) 5040 (%i4) fac(13); (%o4) 6227020800 (%i5) 13! (%o5) 6227020800
Rekursion am Beispiel der Fibonacci-Folge.
(%i1) fib(n) := if n > 2 then fib(n - 1) + fib(n - 2) elseif n = 2 then 1 elseif n =1 then 1;
(%o1) fib(n) := if n > 2 then fib(n - 1) + fib(n - 2) elseif n = 2 then 1
elseif n = 1 then 1
(%i2) fib(3);
(%o2) 2
(%i3) fib(9);
(%o3) 34
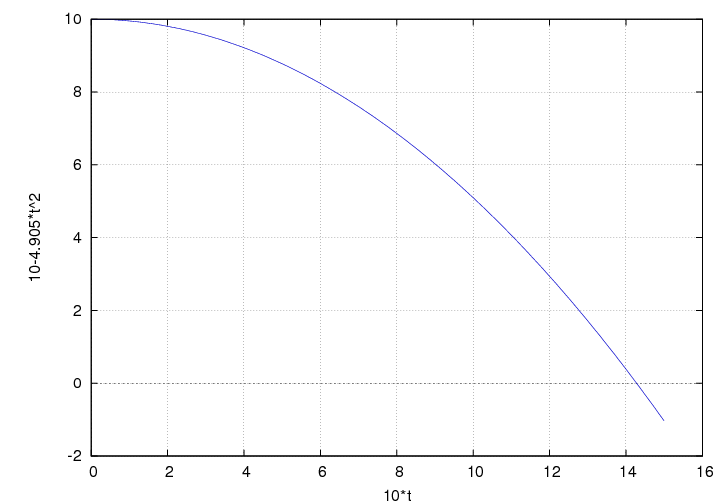
Darstellung einer Wurfparabel unter Vernachlässigung des Luftwiderstandes.
(%i1) v0 : 10 ;
(%o1) 10
(%i2) y0 : 10;
(%o2) 10
(%i3) g : 9.81;
(%o3) 9.810000000000001
(%i4) x(t) := v0*t;
(%o4) x(t) = 10 t
(%i5) y(t) := (- g * t^2)/2 + y0;
2
(%o5) y(t) = 10 - 4.905 t
(%i6) plot2d ([parametric , x(t) , y(t), [t,0,1.5 ] ,[nticks, 200]]);
Lösung eines 3-reihigen linearen Gleichungssystems. Dazu werden zuerst die drei Gleichungen in den Variablen x1, x2 und x3 definiert. Anschliessend wird mittels linsolve gelöst. Das System ist linear abhängig und hat unendlich viele Lösungen. Deswegen taucht in der Lösung der freie Parameter r1 auf.
in (%i5) und folgenden in/output wird gezeigt wie die Koeffzientenmatrix nach Anwendung des Gaussschen Eliminerierungsverfahrens aussieht. Dazu wird der Befehl echelon benutzt. Dieser normiert ausserdem den jeweils ersten Eintrag in einer Zeile der nicht Null ist auf Eins.
(%i1) e1 : x1 + 2*x2 + 3*x3 = 1;
(%o1) 3 x3 + 2 x2 + x1 = 1
(%i2) e2 : 3*x1 + x2 + 2*x3 = 2;
(%o2) 2 x3 + x2 + 3 x1 = 2
(%i3) e3 : 4*x1 + 3*x2 + 5*x3 = 3;
(%o3) 5 x3 + 3 x2 + 4 x1 = 3
(%i4) linsolve([e1,e2,e3],[x1,x2,x3]);
Dependent equations eliminated: (3)
%r1 - 3 7 %r1 - 1
(%o4) [x1 = - -------, x2 = - ---------, x3 = %r1]
5 5
(%i5) mat : matrix([1,2,3],[3,1,2],[4,3,5]);
[ 1 2 3 ]
[ ]
(%o5) [ 3 1 2 ]
[ ]
[ 4 3 5 ]
(%i6) echelon(mat);
[ 1 2 3 ]
[ ]
[ 7 ]
(%o6) [ 0 1 - ]
[ 5 ]
[ ]
[ 0 0 0 ]
/* Definiere Matrix */ hm : matrix([a,b],[b,a]); /* Eigenwerte */ eigenvalues(hm); /* Eigenvektoren */ uev : eigenvectors(hm)[2]; evec1 : flatten(uev[1]); evec2 : flatten(uev[2]); /* Normierte Eigenvektoren */ uev : uniteigenvectors(hm)[2]; evec1 : flatten(uev[1]); evec2 : flatten(uev[2]); /* Diagonalisierung */ smat : matrix(evec1,evec2); expand( smat.hm.transpose(smat) );
This webpage has been created by DK.
* Beitrag von Markus Dieckmann im Rahmen eines Schülerpraktikums, März/April 2009.